Memahami Data¶

Macam macam Data¶

Dalam data data mining dan maha datar, Anda akan menemukan banyak jenis data yang berbeda, dan masing-masing cenderung membutuhkan alat dan teknik yang berbeda. Macam macam data dikelompokkan sebagai berikut:

• Data terstruktur (structured)
• Data tidak terstruktur(unstructured
• Data bahasa alami(Natural Language)
• Data yang dibangkit oleh Mesin (Machined-Generated)
• Data Audio, Video,Citra
• Data Streamming
• Data berbasis Graph(Graph-based)

Data Terstruktur¶

Data terstruktur adalah data yang bergantung pada model data dan yang dinyatakan dalam bentuk tabel dengan atribut} (kolom) dan baris. Data terstruktur mudah disimpan dalam database dalam bentuk tabel atau file excel (Ms Office), SQl (structure Query Language)sehingga mudah dilakukan query terhadap data tersebut. Tetapi realitanya banyak data yang ada dalam dalam bentuk data tidak terstruktur karena data dihasilkan oleh manusia dan mesin

Macam- macam atribut¶

Atribut adalah data yang mewakili karakteristik atau fitur dari objek data. Atribut bisa disebut juga dengan dimensi, fitur, dan variabel yang istilah itu sering digunakan literatur. Dimensi istilah yang biasanya digunakan dalam data warehouse. Dalam literatur pembelajaran mesin cenderung menggunakan istilah fitur, sementara dalam bidang statistik lebih memilih menggunakan istilah variabel. Dalam penambangan data atau data miniing dan database biasa menggunakan istilah atribut atau fitur , dan dalam buku ini juga menggunakan istilah atribut atau fitur. Contoh atribut-atribut yang menggambarkan objek pelanggan dapat mencakup, misalnya ID pelanggan, nama, dan alamat. Nilai yang diamati untuk atribut tertentu dikenal sebagai nilai observasi. Sekumpulan atribut yang digunakan untuk menggambarkan objek disebut disebut dengan vektor atribut (atau vektor fitur. Distribusi data yang melibatkan satu atribut (atau variabel) disebut univariat. Distribusi bivariat melibatkan dua atribut, dan seterusnya. Jenis atribut ditentukan oleh nilai-nilai pada atribut tersebut yang mungkin nominal, biner,atau ordinal, atau numerik. Pada subbagian berikut, kami perkenalkan nilai nilai tersebut

Macam macam tipe data atribut¶

• Atribut Nominal

Nilai atribut nominal adalah simbol ataunama barang. Setiap nilai mewakili beberapa jenis kategori, kode, atau status, dan Atribut nominal juga disebut kategori. Nilai-nilainya tidak memiliki tingkatan nilai. Dalam ilmu komputer, nilainya juga dikenal sebagai enumerasi

Contoh :

Misalkan warna rambut dan status perkawinan adalah dua atribut dari data orang. Nilai yang mungkin untuk warna rambut adalah hitam, coklat, pirang, merah, hitam pucat, abu-abu, dan putih. Status perkawinan memiliki nilai atribut lajang, menikah, bercerai, dan janda. Baik warna rambut maupun status perkawinan adalah atribut nominal. Contoh lain dari atribut nominal adalah atribut pekerjaan dengan nilai-nilainya adalah guru, dokter gigi, programmer, petani, dan sebagainya

• Atribut Biner

Atribut biner adalah atribut nominal dengan hanya dua kategori atau status: 0 atau 1, di mana 0 biasanya berarti atribut itu tidak ada, dan 1 berarti itu ada. Atribut Biner disebut sebagai Boolean jika dinyatakan dengan benar (true) dan salah(false)

Contoh :

Terdapat atribut yang menggambarkan merokok pada pasien, 1 menunjukkan bahwa pasien merokok,sementara 0 menunjukkan bahwa pasien tidak merokok. Demikian pula, seandainya ada pasien menjalani tes medis yang memiliki dua kemungkinan hasil. Atribut Tes medis bersifat biner, dengan nilai 1 berarti hasil tes untuk pasien positif, sedangkan 0 berarti hasilnya negatif. Atribut biner simetris jika keduanya emiliki nilai bobot yang sama; Artinya, tidak ada kekhususan mengenai hasil mana yang harus dikodekan sebagai 0 atau 1. Misalkan atribut gender yang dengan nila atributnya laki dan perempuan. Atribut biner adalah asimetris jika hasil dari nilai nilainya tidak sama pentingnya seperti hasil positif dan negatif dari tes medis untuk HIV. Dengan mengkodekan hasil yang paling penting, biasanya 1 (mis., HIV positif) dan yang lainnya dengan 0 (mis., HIV negatif)

• Atribut ordinal

Atribut ordinal adalah atribut dengan nilai yang memiliki arti urutan atau peringkat di antara nilai nilai yang ada, tapi besarnya nilai yang berurutan tersebut tidak diketahui. Ukuran kecenderungan terpusat dari atribut ordinal dapat diwakili oleh modus dan median median (nilai tengah), tetapi tidak untuk nilai rata-rata.Perlu diperhatikan bahwa atribut nominal, biner, dan ordinal bersifat kualitatif. Artinya, atribut-atribut tersebut hanya menjelaskan sebuah fitur dari suatu objek tanpa memberikan ukuran atau kuantitas yang sebenarnya. Nilai-nilai atribut kualitatif biasanya merupakan katakata yang mewakili kategori

Contoh:

Atribut ordinal Misalkan ukuran minuman yang tersedia di sebuah restoran cepat saji. Atribut nominal ini memiliki tiga nilai yang mungkin: kecil, sedang, dan besar. Nilai memiliki arti urutan yang (yang sesuai dengan ukuran minuman). Contoh atribut ordinal lainnya adalah pangkat dan jabatan profesi. Atribut ordinal berguna untuk melakukan penilaian subjektif terhadap kualitas sesuatu objek yang tidak dapat diukur secara obyektif; atribut ordinal sering digunakan dalam survei untuk peringkat. Dalam satu survei, para peserta diminta untuk menilai tingkat kepuasan mereka sebagai pelanggan.Kepuasan pelanggan memiliki kategori ordinal berikut ini: 0: sangat tidak puas,1: agak tidak puas, 2: netral, 3: puas, dan 4: sangat puas. Atribut ordinal juga dapat diperoleh dari iskritisasi nilai atribut numerik dengan membagi rentang nilai menjadi urutan kategoria

• Atribut Numerik

Atribut numerik bersifat kuantitatif; Artinya, ini adalah kuantitas yang terukur, yang dinyatakan dengan bilangan bulat atau nilai riel. Atribut numerik dapat Atribut Skala Interval(interval-scaled) atau skala ration (ratio-scaled)

• Atribut skala interval diukur pada dengan skala unit ukuran yang sama. Nilai - nilai Interval berskala memiliki urutan dan bisa positif, 0, atau negatif. Jadi, selain untuk memberikan peringkat nilai, atribut semacam itu memungkinkan kita untuk membandingkan dan mengukur perbedaan antar nilai

Contoh:

Atribut suhu adalah Skala interval. Misalkan kita memiliki nilai suhu di luar ruangan untuk beberapa hari yang berbeda dari suatu objek. Dengan mengurutkan nilai, kita mendapatkan peringkat objek yang berkenaan dengan suhu. Selain itu, kita bisa mengukur perbedaan antara nilai.Misalnya, a suhu 20o C adalah lima derajat lebih tinggi dari suhu 15oC. Contoh lain kalender tahun adalah. Misalnya, tahun 2002 dan 2010 terpisah delapan tahun. Karena atribut skala interval adalah numerik, kita dapat menghitung nilai ratarata, ukuran median dan modus dari kecenderungan terpusat

• Atribut Skala Ratio Atribut skala rasio adalah atribut numerik dengan melekat titik nol pada nilai atribut tersebut. Artinya, jika pengukuran adalah berskala rasio, kita dapat dapat mengatakan berapa kali dari nilai yang lain atau rasio dari nilai yang lain. Selain itu, nilai yang dipesan, dan kita juga bisa menghitung selisih antara nilai, serta mean, median, dan modus

Contoh

Atribut tentang pengukuran berat badan, tinggi badan, jumlah kata dalam dokumen

Data Tidak Terstruktur¶

Data tidak terstruktur adalah data yang tidak mudah dimasukkan ke dalam model data karena isi/kontennya spesifik atau bervariasi. Salah satu contoh data tidak terstruktur adalah data email. Meskipun email berisi elemen terstruktur seperti pengirim, judul, dan isi teks, terlalu banyak variasi dari isi yang terkandung dalamnya diantaranya dialek bahasa yang dipakai dan sebagainya. Email juga salah satu contoh data bahasa alami

Bahasa Alami¶

Dalam neuropsikologi , linguistik , dan filsafat bahasa , bahasa alami atau bahasa biasa adalah bahasa yang telah berevolusi secara alami pada manusia melalui penggunaan dan pengulangan tanpa perencanaan. Bahasa alami berbeda dengan bahasa yang dibangun untuk memprogramna komputer atau membangun logika nalar. Bahasa alami dikenal sebagai bahasa manusia misal bahasa indonesia, bahasa inggris dan lain lain. Didalam pemrosesan bahasa alami diperluangan pengetahuan ilmu linguistics, semantics, statistics and machine learning.Dengan pemrosesan bahasa alami membantu komputer untuk memahami bahasa yang telah diucapkan oleh manusia

Data yang dibangkitkan oleh Mesin¶

Data yang dibangkitkan oleh mesin secara otomatis tanpa intervensi manusia. Data ini terus menerus dibangkitkan selama proses tertentu sedang berjalan. Misalkan data weblog dari mesin server yang dihasilkan dari hasil transaksi user dengan sistem web. Contoh lain adalah data yang dihasilkan dari implementasi internet of things misal perekaman suhu udara dan kelembaban udara dari daerah tertentu yang terhubung dengan pusat penyimpanan data tersebut.

Data jaringan atau data berbasis Graph¶

Data graph adalah data yang dinyatakan dengan graph yang dalam matematika mengacu pada konsep teori graph. Data ini menunjukkan keterhubungan antara objek objek atau relasi antar objek objek dengan menggunakan struktur node, edge, dan karakteristik/sifat keterhubungan antar objek tersebut. Salah satu data graph adalah data keterhubungan orang dalam media sosial. Dengan memanfaatkan data graph media sosial kita dapat mengukur ukuran ukuran tertentu berdasarkan struktur yang dibentuknya. Misalkan menentukan pengaruh orang dalam struktur jaringan tersebut, apakah termasuk orang penting/berpengaruh atau bukan. Gambar berikut menunjukkan contoh data graph

Database graph dapat digunakan untuk menyimpan data berbasis graph dan mengunakan query tertentu yaitu SPARQL

Data Audio,Vidio dan Citra¶

Dengan perkembangan teknologi implementasi multimedia yang sangat pesat saat,data audio,video dan citra cukup besar dihasilkan dari transaksi bisnis. Dengan besarnya data yang dihasilkan membutuhkan proses pengolahan spesifik dari data tersebut untuk dimanfaatkan terutama dalam analisa data sain. Diantara pemanfaatan data mulitimedia tersebut adalah pengenalan objek, pengenala suara, segmentasi citra satelit dan banyak analisa lain yang dihasilkan dari data multimeda tersebut.

Data streamming¶

Data Streaming adalah data yang dihasilkan secara terus-menerus oleh ribuan sumber data, yang biasanya mengirimkan catatan data secara bersamaan, dan dalam ukuran kecil (urutan Kilobyte). Data streaming mencakup berbagai macam data seperti logfile yang dihasilkan oleh pelanggan aplikasi seluler atau website Anda, transaksi e-commerce, informasi dari jejaring sosial, data geospasial, dan perangkat sensor yang terhubung atau instrumentasi di pusat data.

Data ini perlu diproses secara berurutan dan bertahap secara record-by-record digunakan untuk berbagai macam analisis misalkan korelasi, agregasi, penyaringan, dan pengambilan sampel. Informasi yang diperoleh dari analisis tersebut memberikan petunjuk terhadap pelanggan mereka seperti penggunaan layanan mereka, aktivitas server, klik website, dan lain lain. Misalnya, dalam bisnis kita dapat melacak perubahan sentimen publik pada merek dan produk mereka dengan menganalisis aliran data media sosial, sehingga dapat merespons secara tepat baik waktu dan tindakan yang harus dilakukan

Distribusi Data¶

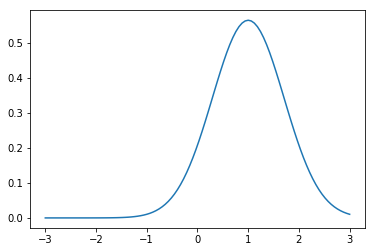
Karakteristik utama dari data adalah distribusi probabilitasnya. Distribusi data yang paling dikenal adalah distribusi normal atau Gaussian. Distribusi ini ditemukan pada sistem fisik dimana data dibangkitkan secara acak. Fungsi dinyatakan dalam bentuk fungsi padat probabilitas(probability density function)

$$ f ( x ) = \frac { 1 } { ( \sigma \sqrt { 2 } \pi ) } \frac { e ^ { - ( x - \mu ) ^ { 2 } } } { ( 2 \sigma ^ { 2 } ) } $$ Dimana $\sigma$ adalah standar deviasi dan $\mu$ adalah mean. Persamaan ini menyatakan peluang variable acak dari suatu data $x$. Kita menyatakan standar deviasi sebagai lebar kurva lonceng dan rata rata sebagai pusat. Kadangkala istilah variance digunakan dan ini adalah kuadrat dari standar deviasi. Standar deviasi pada dasarnya mengukur bagaimana sebaran data.

Untuk memahami lebih jelasnya bagaimana fungsi tersebut digambarkan, berikut implementasinya data dengan distribusi normal yang memiliki rata-rata 1 dan variansinya 0.5

Statistik Deskriptif¶

Ukuran Kecenderungan Terpusat¶

Rata-rata (Mean)¶

Pada bagian ini, kami melihat cara untuk mengukur kecenderungan pusat data. Misalkan kita mempunyai atribut hasil pretest yang dinyatakan dengan atribut X. Misalkan $x_1, x_2, ..., x_N$ menjadi himpunan nilai N yang diamati atau pengamatan untuk X. Di sini, nilai-nilai ini juga dapat disebut set data (untuk X). Jika kita merencanakan pengamatan untuk nilai pretest, di mana sebagian besar nilai berada? Ini memberi kita gambaran tentang kecenderungan pusat dari data. Ukuran kecenderungan pusat data ukurannya adalah rata-rata(mean), median, modus (mode), dan midrange. Atribut numerik yang paling umum dan efektif dari "pusat" dari set data adalah mean (aritmatika). Misalkan $x_1, x_2, ..., x_N$ menjadi satu set nilai N atau pengamatan, Rata-rata dari nilai pretes dinyatakan dengan

Kadang-kadang, setiap nilai $x_i$ dalam satu data dapat dikaitkan dengan bobot $w_i$ untuk $i= 1, .., N$. Bobot tersebut mencerminkan signifikansi, kepentingan, atau frekuensi kejadian yang melekat pada masing masing nilai. Dalam hal ini, kita dapat menghitungnya dengan

Meskipun rata-rata adalah jumlah yang sangat berguna untuk menggambarkan kumpulan data, itu tidak selalu cara terbaik untuk mengukur pusat data. Masalah utama dengan mean adalah sensitivitasnya terhadap nilai ekstrim (mis., outlier). Bahkan beberapa nilai ekstrem saja dapat merusak mean. Misalnya, gaji rata-rata di suatu perusahaan mungkin sangat besar didorong oleh beberapa manajer bergaji tinggi. Demikian pula, nilai rata-rata kelas di ujian dapat rata-rata rendah karena beberapa ada beberap skor nilai saja yang sangat rendah. Untuk mengimbangi efek tersebut kita bisa menggunakan rata-rata yang dipangkas (trimmed mean), yang merupakan rata-rata yang diperoleh setelah memangkas nilai paling tinggi dan nilai yang paling rendah. Untuk contoh, kita dapat mengurutkan nilai gaji yang diamati kemudian menghapus 2% atas dan bawah nilai tersebut sebelum menghitung mean. Kita harus menghindari pemotongan bagian yang terlalu besar (seperti 20%) pada kedua ujungnya, karena hal ini dapat mengakibatkan hilangnya informasi yang berharga)

Median¶

Untuk data miring (asimetris), ukuran pusat data yang lebih baik adalah median, yang merupakan nilai tengah dalam satu set nilai data yang diurutkan. Ini adalah nilai yang memisahkan separuh data yang lebih tinggi dari data tersebut dan sebagian data yang lebih rendah dari data tersebut. Dalam probabilitas dan statistik, median umumnya berlaku untuk data numerik; namun, kami dapat memperluas konsep menjadi data ordinal. Misalkan kumpulan N data yang diberikan untuk atribut X diurutkan dalam urutan naik. Jika N ganjil, maka median adalah nilai tengah dari data yang ordinal. Jika N adalah genap, maka mediannya tidak unik; dihitung dengan rata rata dari nilai $(\frac{N}{2}+1) +(\frac{N}{2}-1) $

Namun pada data berkelompok, dengan data yang berbentuk kelas interval, kita tidak bisa langsung mengetahui nilai median jika kelas mediannya sudah diketahui dengan formula $$ M e=x_{i j}+\left(\frac{\frac{n}{2}-f_{k i j}}{f_{i}}\right) p $$

Contoh

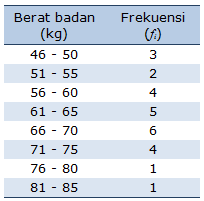
Mode adalah ukuran lain dari kecenderungan sentral. Mode (modus) untuk satu set data adalah nilai yang paling sering terjadi di set. Oleh karena itu, dapat ditentukan untuk atribut kualitatif dan kuantitatif. Dimungkinkan untuk frekuensi terbesar untuk bersesuaian beberapa nilai berbeda, yang menghasilkan lebih dari satu mode. Kumpulan data dengan satu, dua, atau tiga mode masing-masing disebut unimodal, bimodal, dan trimodal. Jika data hanya mengandung nilai data terjadi hanya sekali, maka tidak ada modus

Untuk data numerik unimodal yang cukup miring (asimetris), kami memiliki hubungan empiris:

Ini menyiratkan bahwa mode untuk kurva frekuensi unimodal yang cukup miring dapat dengan mudah didekati jika nilai rata-rata dan median diketahui.

Mengukur Sebaran Data¶

Kita sekarang membahas ukuran ukuran untuk menilai dispersi atau penyebaran data numerik. Ukuran-ukuran itu adalah rentang (range), kuantil, kuartil, persentil, dan rentang interkuartil. Semua itu adalah ringkasan lima angka, yang dapat ditunjukkan dengan boxplot, berguna dalam mengidentifikasi pencilan (outlier). Varians dan standar deviasi juga menunjukkan sebaran distribusi data.

Rentang (Range), Quartil, and Rentang Interquartile¶

Misalkan $x_1, x_2, .. x_N$ adalah sekumpulan pengamatan untuk atribut numerik, $X$. Rentang adalah selisih antara nilai terbesar (maks ()) dan terkecil (min ()). Misalkan data untuk atribut X diurutkan dalam urutan naik.Bagilah data berdasarkan titik titik tertentu sehingga membagi distribusi data ukuran yang sama, seperti pada Gambar dibawah. Titik data ini disebut kuantil. 2-quantile adalah titik data yang membagi bagian bawah dan atas dari distribusi data. Ini sama dengan median. 4-kuantil adalah tiga titik data yang membagi distribusi data menjadi empat bagian yang sama; setiap bagian mewakili seperempat dari distribusi data. Ini lebih sering disebut sebagai kuartil. 100-kuantil lebih sering disebut sebagai persentil; mereka membagi distribusi data menjadi 100 data berukuran sama. Median, kuartil, dan persentil adalah bentuk kuantil yang paling banyak digunakan.

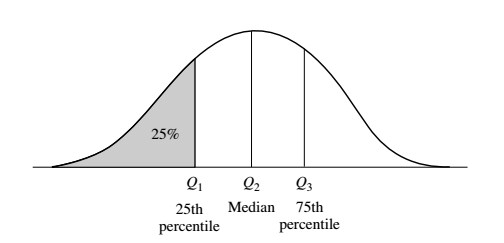
Kuartil memberikan gambaran pusat distribus, penyebaran, dan bentuk distribusi. Kuartil satu, dilambangkan oleh Q1, adalah persentil ke-25. Nilai ini menunjukan 25% terendah dari data. Kuartil ketiga, dilambangkan oleh Q3, adalah persentil ke-75 - itu memisahkan data 75% dari terendah data (atau 25% dari tertinggi data. Kuartil kedua adalah persentil ke-50 atau median dari distribusi data.

Jarak antara kuartil pertama dan ketiga adalah ukuran yang menyatakan rentang yang dicakup oleh bagian tengah data. Jarak ini disebut rentang interkuartil (IQR) dan dinyatakan dengan

Dengan ukuran a kuartil Q1 dan Q3, dan median kita dapat mengidentifikasikan ada tidaknya pencilan (outlier) pada suatu data. Data pencilan atau outlier nilai data biasanya ada di setidaknya 1,5 × IQR di atas kuartil ketiga atau di bawah kuartil pertama

Karena Q1, median, dan Q3 tidak berisi informasi tentang titik akhir (mis., Ekor) data, ringkasan yang lebih lengkap dari bentuk distribusi dapat diperoleh dengan memberikan nilai data terendah dan tertinggi juga. Ini dikenal sebagai ringkasan lima angka. Ringkasan lima nomor distribusi terdiri dari median (Q2), kuartil Q1 dan Q3, dan data terkecil dan terbesar( Minimum, Q1, Median, Q3, Maksimum)

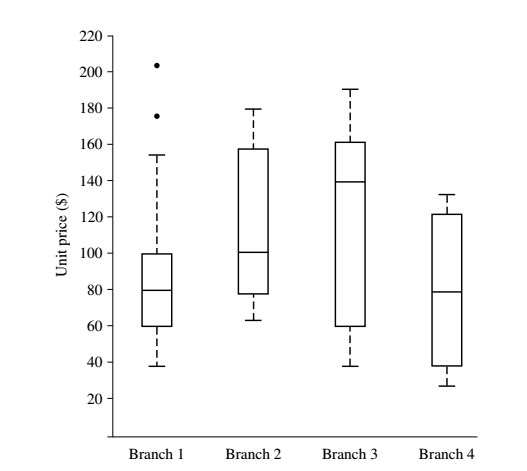
Boxplots adalah cara populer untuk memvisualisasikan distribusi. Boxplot menggabungkan ringkasan lima angka sebagai berikut: - Ujung kotak adalah kuartil dan panjang kotak adalah rentang interkuartil. - Median ditandai dengan garis di dalam kotak. - Dua garis (disebut whiskers) di luar kotak memanjang ke pengamatan terkecil (Minimum) dan terbesar (Maksimum)

Outlier biasanya ada di dibawah $Q_1 – 1.5 \times IQR$ dan diatas $ Q_3 + 1.5 \times IQR$

Variansi dan Standar Deviasi¶

Variansi dan standar deviasi adalah ukuran penyebaran data. Nilai-nilai tersebut menunjukkan bagaimana penyebaran distribusi data. Standar Deviasi yang rendah berarti bahwa pengamatan data cenderung sangat dekat dengan rata-rata, sedangkan deviasi standar yang tinggi menunjukkan data tersebar di sejumlah nilai-nilai besar.

Varian dari pengamatan $N, x_1, x_2, ..., x_N$, untuk atribut numerik X adalah

di mana $ \overline { x } $ adalah nilai rata-rata dari pengamatan, Standar deviasi,$\sigma $, dari pengamatan adalah akar kuadrat dari variansi, $\sigma^2$

Sifat dasar dari standar deviasi, $\sigma$, sebagai ukuran penyebaran data adalah sebagai berikut:

• Ukuran $\sigma$ mengeukur sebaran disekitar rata-rata dan harus dipertimbangkan bila rata-rata dipilih sebagai ukuran pusat data
• $\sigma = 0$ hanya jika tidak ada penyebaran data, hanya terjadi ketika semua pengamatan memiliki nilai sama, Jika tidak maka $\sigma > 0$

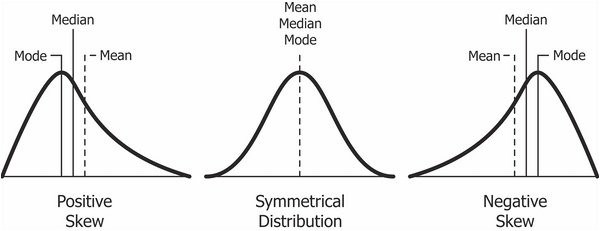
Skewness¶

Derajat distorsi dari kurva lonceng simetris atau distribusi normal. Ini mengukur kurangnya simetri dalam distribusi data Untuk menghitung derajat distorisi dapat menggunakan Koefisien Kemencengan Pearson yang diperoleh dengan menggunakan nilai selisih rata-rata dengan modus dibagi simpangan baku. Koefisien Kemencengan Pearson dirumuskan sebagai berikut

dengan $$ \overline{X}-M o \approx 3(\overline{X}-M e) $$

maka

Implementasi¶

Untuk implementasi silahkan unduh data.csv

import pandas as pd
from scipy import stats
df=pd.read_csv("data.csv",usecols=[0])

print("jumlah data  ",df['NilaiPreTest'].count())
print("rata-rata   ",df['NilaiPreTest'].mean())
print("nila minimal ",df['NilaiPreTest'].min())
print("Q1       ",df['NilaiPreTest'].quantile(0.25))
print("Q2          ",df['NilaiPreTest'].quantile(0.5))
print("Q3          ",df['NilaiPreTest'].quantile(0.75))
print("Nilai Max   ",df['NilaiPreTest'].max())
print("kemencengan","{0:.2f}".format(round(df['NilaiPreTest'].skew(),2)))
mode=stats.mode(df)
print("Nilai modus {} dengan jumlah {}".format(mode.mode[0], mode.count[0]))
print("kemencengan          " ,"{0:.6f}".format(round(df['NilaiPreTest'].skew(),6)))
print("Standar Deviasi   ","{0:.2f}".format(round(df['NilaiPreTest'].std(),2)))
print("Variansi         ","{0:.2f}".format(round(df['NilaiPreTest'].var(),2)))

Mengukur Jarak Data¶

Mengukur Jarak Tipe Numerik¶

Shirkhorshidi, A. S., Aghabozorgi, S., & Wah, T. Y. (2015). A comparison study on similarity and dissimilarity measures in clustering continuous data. PloS one, 10(12), e0144059.

Salah satu tantangan dalam era ini dengan datatabase yang memiliki banyak tipe data. Mengukur jarak adalah komponen utama dalam algoritma clustering berbasis jarak. Alogritma seperit Algoritma Partisioning misal K-Mean, K-medoidm dan fuzzy c-mean dan rough clustering bergantung pada jarak untuk melakukan pengelompokkan

Sebelum menjelaskan tentang beberapa macam ukuran jarak, kita mendefinisikan terlebih dahulu yaiut $v_1, v_2$ menyatakandua vektor yang menyatakan $v_1 = {x_1, x_2, . . ., x_n}, v_2 ={y_1, y_2, . . ., y_n},$ dimana $x_i, y_i$ disebut attribut. Ada beberapa ukuran similaritas datau ukuran jarak, diantaranya

Minkowski Distance¶

Kelompk Minkowski diantaranya adalah Euclidean distance dan Manhattan distance, yang menjadi kasus khusus dari Minkowski distance. Minkowski distance dinyatakan dengan

diman $m$ adalah bilangan riel positif dan $x_i$ dan $ y_i$ adalah dua vektor dalam runang dimensi $n$ Implementasi ukuran jarak Minkowski pada model clustering data atribut dilakukan normalisasi untuk menghindari dominasi dari atribut yang memiliki skala data besar.

Manhattan distance¶

Manhattan distance adalah kasus khsusu dari jarak Minkowski distance pada m = 1. Seperti Minkowski Distance, Manhattan distance sensitif terhadap outlier. BIla ukuran ini digunakan dalam algoritma clustering , bentuk cluster adalah hyper-rectangular. Ukuran ini didefinisikan dengan

Euclidean distance¶

Jarak yang paling terkenal yang digunakan untuk data numerik adalah jarak Euclidean. Ini adalah kasus khusus dari jarak Minkowski ketika m = 2. Jarak Euclidean berkinerja baik ketika digunakan untuk kumpulan data cluster kompak atau terisolasi . Meskipun jarak Euclidean sangat umum dalam pengelompokan, ia memiliki kelemahan: jika dua vektor data tidak memiliki nilai atribut yang sama, kemungkin memiliki jarak yang lebih kecil daripada pasangan vektor data lainnya yang mengandung nilai atribut yang sama. Masalah lain dengan jarak Euclidean sebagai fitur skala terbesar akan mendominasi yang lain. Normalisasi fitur kontinu adalah solusi untuk mengatasi kelemahan ini.

Average Distance¶

Berkenaan dengan kekurangan dari Jarak Euclidian Distance diatas, rata rata jarak adala versi modikfikasid ari jarak Euclidian untuk memperbaiki hasil. Untuk dua titik $x,y$ dalam ruang dimensi $n$, rata-rata jarak didefinisikan dengan

Weighted euclidean distance¶

Jika berdasarkan tingkatan penting dari masing masing atribut ditentukan, maka Weighted Euclidean distance adalah modifikisasi lain dari jarak Euclidean distance yang dapat digunakan. Ukuran ini dirumuskan dengan

$$ d _ { w e } = \left ( \sum _ { i = 1 } ^ { n } w _ { i } ( x _ { i } - y _ { i } \right) ^ { 2 } ) ^ { \frac { 1 } { 2 } } $$ dimana $w_i$ adalah bobot yang diberikan pada atribut ke i.

Chord distance¶

Chord distance adalah salah satu ukuran jarak modifikasi Euclidean distance untuk mengatasi kekurangan dari Euclidean distance. Ini dapat dipecahkan juga dengan menggunakan skala pengukuran yang baik. Jarak ini dapat juga dihitung dari data yang tidak dinormalisasi . Chord distance didefinisikan dengan

dimana $\| x \|_ {2}$ adalah $L^{2} \text {-norm} \| x \|_{2} = \sqrt { \sum_{ i = 1 }^{ n }x_{i}^{2}}$

Mahalanobis distance¶

Mahalanobis distance berdasarkan data berbeda dengan Euclidean dan Manhattan distances yang bebas antra data dengan data yang lain. Jarak Mahalanobis yang teratur dapat digunakan untuk mengekstraksi hyperellipsoidal clusters. Jarak Mahalanobis dapat mengurangi distorsi yang disebabkan oleh korelasi linier antara fitur dengan menerapkan transformasi pemutihan ke data atau dengan menggunakan kuadrat Jarak mahalanobis. Mahalanobis distance dinyatakan dengan

diman $S$ adalah matrik covariance data.

Cosine measure¶

Ukuran Cosine similarity lebih banyak digunakan dalam similaritas dokumen dan dinyatakan dengan

dimana $\|y\|_{2}$ adalah Euclidean norm dari vektor $y=(y_{1} , y_{2} , \dots , y_{n} )$ didefinisikan dengan $\|y\|_{2}=\sqrt{ y _ { 1 } ^ { 2 } + y _ { 2 } ^ { 2 } + \ldots + y _ { n } ^ { 2 } }$

Pearson correlation¶

Pearson correlation banyak digunakan dalam data expresi gen. Ukuran similaritas ini menghitung similaritas antara duan bentuk pola expresi gen. Pearson correlation didefinisikan dengan

The Pearson correlation kelemahannya adalah sensitif terhadap outlier

Mengukur Jarak Atribut Binary¶

Mari kita lihat similaritas dan desimilirity untuk objek yang dijelaskan oleh atribut biner simetris atau asimetris. Aatribut biner hanya memiliki dua status: 0 dan 1 Contoh atribut perokok menggambarkan seorang pasien, misalnya, 1 menunjukkan bahwa pasien merokok, sedangkan 0 menunjukkan pasien tidak merokok. Memperlakukan atribut biner sebagai atribut numerik tidak diperkenankan. Oleh karena itu, metode khusus untuk data biner diperlukan untuk membedakan komputasi.

Jadi, bagaimana kita bisa menghitung ketidaksamaan antara dua atribut biner? ”Satu pendekatan melibatkan penghitungan matriks ketidaksamaan dari data biner yang diberikan. Jika semua atribut biner dianggap memiliki bobot yang sama, kita memiliki tabel kontingensi $2 \times 2$ di mana $q$ adalah jumlah atribut yang sama dengan 1 untuk kedua objek $i$ dan $j$, $r$ adalah jumlah atribut yang sama dengan 1 untuk objek $i$ tetapi 0 untuk objek $j$, $s$ adalah jumlah atribut yang sama dengan 0 untuk objek $i$ tetapi 1 untuk objek $j$, dan $t$ adalah jumlah atribut yang sama dengan 0 untuk kedua objek $i$ dan $j$. Jumlah total atribut adalah $p$, di mana $p=q+r+s+t$

Ingatlah bahwa untuk atribut biner simetris, masing-masing nilai bobot yang sama.Dissimilarity yang didasarkan pada atribut aymmetric binary disebut symmetric binary dissimilarity. Jika objek i dan j dinyatakan sebagai atribut biner simetris, maka dissimilarity antar$i$ dan $j$ adalah

Untuk atribut biner asimetris, kedua kondisi tersebut tidak sama pentingnya, seperti hasil positif (1) dan negatif (0) dari tes penyakit. Diberikan dua atribut biner asimetris, pencocokan keduanya 1 (kecocokan positif) kemudian dianggap lebih signifikan daripada kecocokan negatif. Ketidaksamaan berdasarkan atribut-atribut ini disebut asimetris biner dissimilarity, di mana jumlah kecocokan negatif, t, dianggap tidak penting dan dengan demikian diabaikan. Berikut perhitungannya

Kita dapat mengukur perbedaan antara dua atribut biner berdasarkan pada disimilarity. Misalnya, biner asimetris kesamaan antara objek $i$ dan $j$ dapat dihitung dengan

Persamaan similarity ini disebut dengan Jaccard coefficient

Mengukur Jarak Tipe categorical¶

Li, C., & Li, H. (2010). A Survey of Distance Metrics for Nominal Attributes. JSW, 5(11), 1262-1269.

Overlay Metric¶

Ketika semua atribut adalah bertipe nominal, ukuran jarak yang paling sederhana adalah dengan Ovelay Metric (OM) yang dinyatakan dengan

dimana $n$ adalah banyaknya atribut, $a_i(x)$ dan $a_i(y)$ adalah nilai atribut ke $i$ yaitu $A_i$ dari masing masing objek $x$ dan $y$, $\delta \ ( a_{ i } ( x ) , a_{ i } ( y ) )$ adalah 0 jika $a _ { i } ( x ) = a _ { i } ( y )$ dan 1 jika sebaliknya.

OM banyak digunakan oleh instance-based learning dan locally weighted learning. Jelas sekali , ini sedikit beruk untuk mengukur jarak antara masing-masing pasangan sample, karena gagal memanfaatkan tambahan informasi yang diberikan oleh nilai atribut nominal yang bisa membantu dalam generalisasi.

Value Difference Metric (VDM)¶

VDM dikenalkan oleh Standfill and Waltz, versi sederhana dari VDM tanpa skema pembobotan didefinsisikan dengan

dimana $C$adalah banyaknya kelas, $P(c|a_i(x))$ adalah probabilitas bersyarat dimana kelas $x$ adalah $c$ dari atribut $A_i$, yang memiliki nilai $a_i(x)$, $P(c|a_i(y))$ adalah probabilitas bersyarat dimana kelas $y$ adalah $c$ dengan atribut $A_i$ memiliki nilai $a_i(y)$

VDM mengasumsikan bahwa dua nilai dari atribut adalah lebih dekat jika memiliki klasifikasi sama. Pendekatan lain berbasi probabilitas adalah SFM (Short and Fukunaga Metric) yang kemudian dikembangkan oleh Myles dan Hand dan didefinisikan dengan

diman probabilitas keanggotaan kelas diestimasi dengan $P(c|x)$ dan $P(c|y)$ didekati dengan Naive Bayes,

Minimum Risk Metric (MRM)¶

Ukuran ini dipresentasikan oleh Blanzieri and Ricci, berbeda dari SFM yaitu meminimumkan selisih antara kesalahan berhingga dan kesalahan asymtotic. MRM meminimumkan risk of misclassification yang didefinisikan dengan

$$ d ( x , y ) = \sum _ { c = 1 } ^ { C } P ( c | x ) ( 1 - P ( c | y ) ) $$

Mengukur Jarak Tipe Ordinal¶

Han, J., Pei, J., & Kamber, M. (2011). Data mining: concepts and techniques. Elsevier.

Nilai-nilai atribut ordinal memiliki urutan atau peringkat, namun besarnya antara nilai-nilai berturut-turut tidak diketahui. Contohnya tingkatan kecil, sedang, besar untuk atribut ukuran. Atribut ordinal juga dapat diperoleh dari diskritisasi atribut numerik dengan membuat rentang nilai ke dalam sejumlah kategori tertentu. Kategori-kategori ini disusun dalam peringkat. Yaitu, rentang atribut numerik dapat dipetakan ke atribut ordinal $f$ yang memiliki $M_f$ state. Misalnya, kisaran suhu atribut skala-skala (dalam Celcius)dapat diatur ke dalam status berikut: −30 hingga −10, −10 hingga 10, 10 hingga 30, masing-masing mewakili kategori suhu dingin, suhu sedang, dan suhu hangat. $M$ adalah jumlah keadaan yang dapat dilakukan oleh atribut ordinalmemiliki. State ini menentukan peringkat $1, ..., M_f$

Perlakuan untuk atribut ordinal adalah cukup sama dengan atribut numerik ketika menghitung disimilarity antara objek. Misalkan $f$ adalah atribut-atribut dari atribut ordinal dari $n$ objek. Menghitung disimilarity terhadap f fitur sebagai berikut:

• Nilai $f$ untuk objek ke-$i$ adalah $x_{if}$, dan $f$ memiliki $M_f$ status urutan , mewakili peringkat $1, .., M_f$ Ganti setiap $x_{if}$ dengan peringkatnya, $r_{if} \in \{1...M_f\}$
• Karena setiap atribut ordinal dapat memiliki jumlah state yang berbeda, diperlukan untuk memetakan rentang setiap atribut ke [0,0, 1.0] sehingga setiap atribut memiliki bobot yang sama. Perl melakukan normalisasi data dengan mengganti peringkat $r_{if}$ dengan $$ z _ { i f } = \frac { r _ { i f } - 1 } { M _ { f } - 1 } $$
• Dissimilarity kemudian dihitung dengan menggunakan ukuran jarak seperti atribut numerik dengan data yang baru setelah ditransformasi $ z _ { i f }$

Menghitung Jarak Tipe Campuran¶

Wilson, D. R., & Martinez, T. R. (1997). Improved heterogeneous distance functions. Journal of artificial intelligence research, 6, 1-34.

Menghitung ketidaksamaan antara objek dengan atribut campuran yang berupa nominal, biner simetris, biner asimetris, numerik, atau ordinal yang ada pada kebanyakan databasae dapat dinyatakan dengan memproses semua tipe atribut secara bersamaan. Salah satu teknik tersebut menggabungkan atribut yang berbeda ke dalam matriks ketidaksamaan tunggal dan menyatakannya dengan skala interval antar $[0,0, 1.0]$. Misalkan data berisi atribut $p$ tipe campuran. Ketidaksamaan (disimilarity ) antara objek $i$ dan $j$ dinyatakan dengan

dimana $\delta_{ij}^{f}=0$ - jika $x_{if}$ atau $x_{jf}$ adalah hilang (i.e., tidak ada pengukuran dari atribut f untuk objek $i$ atau objek $j$)

• jika $x_{if}=x_{jf}=0$ dan
• atribut $f$ adalah binary asymmetric,

selain itu $\delta_{ij}^{f}=1$

Kontribusi dari atribut $f$ untuk dissimilarity antara i dan j (yaitu.$d_{ij}^{f}$) dihitung bergantung pada tipenya,

• Jika $f$ adalah numerik, $d_{ij}^{f}=\frac{ \|x _{if}-x_{jf}\|}{max_hx_{hf}-min_hx{hf}}$, di mana h menjalankan semua nilai objek yang tidak hilang untuk atribut f
• Jika $f$ adalah nominal atau binary,$d_{ij}^{f}=0 $jika $x_{if}=x_{jf}$, sebaliknya $d_{ij}^{f}=1$
• Jika $f$ adalah ordinal maka hitung rangking $r_{if}$ dan $\mathcal z_{if}=\frac {r_{if}-1}{M_f-1}$ , dan perlakukan $z_{if}$ sebagai numerik.